下篇：平衡二叉树
二叉查找树
二叉查找树（Binary Search Tree），或者是一颗空树，或者是具有下列性质的二叉树：
1、若它的左子树不空，则其左子树上的所有结点的值均小于它根结点的值；
2、若它的右子树不空，则其右子树上的所有结点的值均大于它根结点的值；
3、它的左、右子树也分别为二叉查找树。
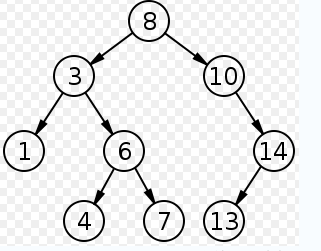
二叉查找树是基于二叉树的，其结点数据结构定义为如下：
/**结点数据结构*/ static class BinaryNode{ T data; BinaryNode left; BinaryNode right; public BinaryNode(T data) { this(data,null,null); } public BinaryNode( T data, BinaryNode left, BinaryNode right) { this.data =data; this.left = left; this.right =right; } public BinaryNode() { data =null; this.left = left; this.right =right; } }
现在明白了什么是二叉查找树，那么二叉查找书的基本操作又是如何来实现的呢？
查找操作
在二叉查找树中查找x的过程如下：
1、若二叉树是空树，则查找失败。
2、若x等于根结点的数据，则查找成功，否则。
3、若x小于根结点的数据，则递归查找其左子树，否则。
4、递归查找其右子树。
根据上述的步骤，写出其查找操作的代码：
/**查找指定的元素,默认从 * 根结点出开始查询*/ public boolean contains(T t) { return contains(t, rootTree); } /**从某个结点出开始查找元素*/ public boolean contains(T t, BinaryNode node) { if(node==null) return false;//结点为空，查找失败 int result = t.compareTo(node.data); if(result>0) return contains(t,node.right);//递归查询右子树 else if(result<0) return contains(t, node.left);//递归查询左子树 else return true; } /** 这里我提供一个对二叉树最大值 最小值的搜索*/ /**找到二叉查找树中的最小值*/ public T findMin() { if(isEmpty()) { System.out.println("二叉树为空"); return null; }else return findMin(rootTree).data; } /**找到二叉查找树中的最大值*/ public T findMax() { if(isEmpty()) { System.out.println("二叉树为空"); return null; }else return findMax(rootTree).data; } /**查询出最小元素所在的结点*/ public BinaryNode findMin(BinaryNode node) { if(node==null) return null; else if(node.left==null) return node; return findMin(node.left);//递归查找 } /**查询出最大元素所在的结点*/ public BinaryNode findMax(BinaryNode node) { if(node!=null) { while(node.right!=null) node=node.right; } return node; } 插入操作
二叉树查找树b插入操作x的过程如下：
1、若b是空树，则直接将插入的结点作为根结点插入。 2、x等于b的根结点的数据的值，则直接返回，否则。 3、若x小于b的根结点的数据的值，则将x要插入的结点的位置改变为b的左子树，否则。 4、将x要出入的结点的位置改变为b的右子树。 代码实现如下：/**插入元素*/ public void insert(T t) { rootTree = insert(t, rootTree); } /**在某个位置开始判断插入元素*/ public BinaryNode insert(T t,BinaryNode node) { if(node==null) { //新构造一个二叉查找树 return new BinaryNode (t, null, null); } int result = t.compareTo(node.data); if(result<0) node.left= insert(t,node.left); else if(result>0) node.right= insert(t,node.right); else ;//doNothing return node; } 删除操作
对于二叉查找树的删除操作（这里根据值删除，而非结点）分三种情况：
不过在此之前，我们应该确保根据给定的值找到了要删除的结点，如若没找到该结点 不会执行删除操作！ 下面三种情况假设已经找到了要删除的结点。 1、如果结点为叶子结点（没有左、右子树），此时删除该结点不会玻化树的结构 直接删除即可，并修改其父结点指向它的引用为null.如下图: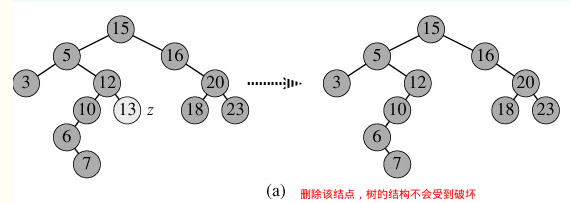
2、如果其结点只包含左子树，或者右子树的话，此时直接删除该结点，并将其左子树 或者右子树设置为其父结点的左子树或者右子树即可，此操作不会破坏树结构。 
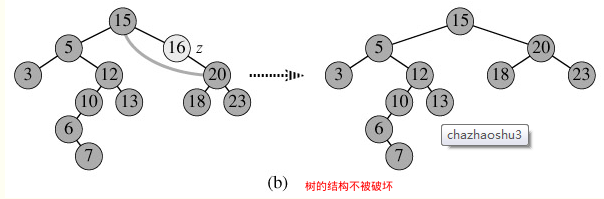3、 当结点的左右子树都不空的时候，一般的删除策略是用其右子树的最小数据 （容易找到）代替要删除的结点数据并递归删除该结点（此时为null），因为
右子树的最小结点不可能有左孩子，所以第二次删除较为容易。
z的左子树和右子树均不空。找到z的后继y，因为y一定没有左子树，所以可以删除y，
并让y的父亲节点成为y的右子树的父亲节点，并用y的值代替z的值.如图：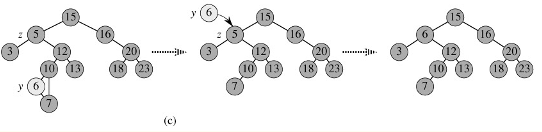
删除操作源码：
/**删除元素*/ public void remove(T t) { rootTree = remove(t,rootTree); } /**在某个位置开始判断删除某个结点*/ public BinaryNode remove(T t,BinaryNode node) { if(node == null) return node;//没有找到,doNothing int result = t.compareTo(node.data); if(result>0) node.right = remove(t,node.right); else if(result<0) node.left = remove(t,node.left); else if(node.left!=null&&node.right!=null) { node.data = findMin(node.right).data; node.right = remove(node.data,node.right); } else node = (node.left!=null)?node.left:node.right; return node; } 完整源码
package com.kiritor; /** * Java实现二叉查找树 * @author Kiritor * @param*/ public class BinarySearchTree > { /**结点数据结构*/ static class BinaryNode { T data; BinaryNode left; BinaryNode right; public BinaryNode(T data) { this(data,null,null); } public BinaryNode( T data, BinaryNode left, BinaryNode right) { this.data =data; this.left = left; this.right =right; } public BinaryNode() { data =null; this.left = left; this.right =right; } } private BinaryNode rootTree; /**构造一颗空的二叉查找树*/ public BinarySearchTree() { rootTree = null; } /**清空二叉查找树*/ public void clear() { rootTree = null; } /**判断是否为空*/ public boolean isEmpty() { return rootTree == null; } /**查找指定的元素,默认从 * 根结点出开始查询*/ public boolean contains(T t) { return contains(t, rootTree); } /**找到二叉查找树中的最小值*/ public T findMin() { if(isEmpty()) { System.out.println("二叉树为空"); return null; }else return findMin(rootTree).data; } /**找到二叉查找树中的最大值*/ public T findMax() { if(isEmpty()) { System.out.println("二叉树为空"); return null; }else return findMax(rootTree).data; } /**插入元素*/ public void insert(T t) { rootTree = insert(t, rootTree); } /**删除元素*/ public void remove(T t) { rootTree = remove(t,rootTree); } /**打印二叉查找树*/ public void printTree() { } /**从某个结点出开始查找元素*/ public boolean contains(T t, BinaryNode node) { if(node==null) return false; int result = t.compareTo(node.data); if(result>0) return contains(t,node.right); else if(result<0) return contains(t, node.left); else return true; } /**查询出最小元素所在的结点*/ public BinaryNode findMin(BinaryNode node) { if(node==null) return null; else if(node.left==null) return node; return findMin(node.left);//递归查找 } /**查询出最大元素所在的结点*/ public BinaryNode findMax(BinaryNode node) { if(node!=null) { while(node.right!=null) node=node.right; } return node; } /**在某个位置开始判断插入元素*/ public BinaryNode insert(T t,BinaryNode node) { if(node==null) { //新构造一个二叉查找树 return new BinaryNode (t, null, null); } int result = t.compareTo(node.data); if(result<0) node.left= insert(t,node.left); else if(result>0) node.right= insert(t,node.right); else ;//doNothing return node; } /**在某个位置开始判断删除某个结点*/ public BinaryNode remove(T t,BinaryNode node) { if(node == null) return node;//没有找到,doNothing int result = t.compareTo(node.data); if(result>0) node.right = remove(t,node.right); else if(result<0) node.left = remove(t,node.left); else if(node.left!=null&&node.right!=null) { node.data = findMin(node.right).data; node.right = remove(node.data,node.right); } else node = (node.left!=null)?node.left:node.right; return node; } public BinaryNode init() { BinaryNode node3 = new BinaryNode (3); BinaryNode node1 = new BinaryNode (1); BinaryNode node4 = new BinaryNode (4,node3,null); BinaryNode node2 = new BinaryNode (2,node1,node4); BinaryNode node8 = new BinaryNode (8); BinaryNode root = new BinaryNode (6,node2,node8); return root; } public void preOrder(BinaryNode node) { if (node != null) { System.out.print(node.data); preOrder(node.left); preOrder(node.right); } } /*简单测试*/ public static void main(String[] args) { BinarySearchTree searchTree = new BinarySearchTree<>(); BinaryNode node= searchTree.init(); searchTree.rootTree=node; searchTree.preOrder(searchTree.rootTree); searchTree.remove(4); searchTree.preOrder(searchTree.rootTree); } }